张广为, 栗苹, 张继豪, 章鸿运, 李国林, 贾瑞丽
(北京理工大学 机电动态控制重点实验室, 北京 100081)
收稿日期:2021-09-27
基金项目:军委科技委基础加强项目(202020201062)
随着微电子技术的飞速发展,引信在技术和形式上得到了快速更新,无线电调频引信向着高载频、超宽带方向发展[1]。太赫兹引信在目标探测、电子对抗等领域具有广阔的应用前景[2-3]。近年来,太赫兹信号源的稳定性和小型化技术逐渐走向成熟,开始应用于近程探测[4-5]。
对于线性调频引信,回波信号时频分析是测距的基础[6-8],信号中的频率成分也反映了面目标的散射特性。太赫兹频段的面目标回波特性目前相关的研究内容较少。时频分析是当今信号处理领域的热点研究问题[9-10]。时频分析的方法主要研究非平稳信号的时变特征,将引信回波信号扩展到二维时频平面上进行特征抓取和观察,从而得到信号频率随时间的变化特征。时频分析的经典方法之一是短时傅立叶变换,其基本思想是利用一个窗函数在信号的时间轴上进行滑动。为解决短时傅里叶的固定窗函数带来的局域频率分辨问题,Daubechies等[11]应用小波变换方法来进行时频分析,结果发现小波变换可以满足实际应用的要求,小波时频分析已经应用引信信号分析中。信号的二次型时频表示是一种更加直观信号频率分布表示方法。物理学家Wigner在量子力学的研究中心中提出了著名的Wigner分布[12-13]。Ville将其引入信号处理领域[14]。Wigner-Ville分布存在严重的交叉项干扰。有学者为抑制交叉项干扰又提出SPWVD、RPWVD、RSWVD等改进方案,都取得了一定的效果。Huang等提出了一种新颖的信号处理方法,被称为Hilbert-Huang变换,该方法包含经验模式分解和希尔伯特谱分析[15]两个部分。
对地的榴弹、迫弹无线电引信而言,依据弹丸与地面的高度作为起爆控制量,利用地面面目标的回波信号特征完成起爆控制,也就是探测的目标是各种地面。主要研究地面的相关散射特性,这也是与其他制导弹药的主要差异[1]。
小波时频方法由窗函数引起的有限数据长度增加了时频特性分析的难度。WVD存在严重的交叉干扰项影响频率成分的判断。本文利用小波时频、WVD、Mor-RPWVD分析方法研究西藏地区高寒干草地和高寒沼泽两种典型面目标回波信号的时频特性,揭示现有时频分析方法应用于太赫兹引信面目标回波分析的局限性和太赫兹引信面目标散射特性,并进行理论解释说明,提出一种新的重排小波- 伪魏格纳时频分析(Mor-RPWVD)方法。Mor-RPWVD引入了距离加权思想和时频信息融合方法,可进一步提高时频分析方法的交叉项干扰抑制能力和能量聚集性。最后利用实测数据验证了Mor-RPWVD分析方法的良好适用性。
1.1 小波时频分析
信号x(t)的连续小波变换定义为
(1)
式中:a为小波尺度;
b为时延;
g(·)为母小波;
*表示共轭。为便于得到非线性信号隐藏的谐波特性,利用Morlet母小波,可以表示为
g(t)=e-t2/2e-iπf0t= e-t2/2(cos(2πf0t)+isin(2πf0t))
(2)
式中:f0为小波的中心频率。小波变化的时频谱称为小波尺度图,其定义如下:
SCAL(a,b)=|W(a,b)|2
(3)
Chui[16]给出了小波变换的时间分辨率Δt和频率分辨率Δf的定义:
Δt=aΔtg,Δf=Δfg/a
(4)
式中:Δtg、Δfg为根据均方测度得到的时域和频域带宽的有效容忍度,
(5)
于是,在时间和频率上的ti时间分辨率和fi频率分辨率为
(6)
1.2 Wigner-Ville分布
Wigner-Ville分布是最有代表性的一种双线性时频分布,不同形式的局部相关函数,可以得到不同的时频分析结果。考虑最简单的局部相关函数,Wigner-Ville分布可以表示为
(7)
式中:Rz(t,τ)为局部相关函数,τ为时延;
δ(·)表示时间冲激函数;
s(·)表示信号;
Rz(t,τ)关于τ的Fourier变换可以表示为
(8)
f为信号频率成分。Wigner-Ville分布是典型的二次型变换,它定义为信号瞬时相关函数的傅立叶变换,反映了信号瞬时时频关系。在式(8)中可以看出,Wigner-Ville分布不含有任何形式的窗函数,避免了时频分辨率和频率分辨率的相互限制。在理论上,对于单频率分量信号,具有最高的时频聚集性。
1.3 Mor-RPWVD时频分析
小波变换的时频分析方法可以有效地描述平稳信号的局部时频特性。对于非平稳信号,由于小波变换将窗函数加到数据中,导致分析时可用的数据长度受到限制,因此运用小波时频分析方法从信号中提取非平稳的低频瞬变频率分量是困难的,而其对非平稳信号中的高频成分具有良好的分析效果。此外,小波分析的时频谱能量聚集差,导致频率分辨率差。
WVD存在严重的交叉干扰项影响频率成分的判断。WVD在时域上加窗会限制有效数据长度,出现与小波时频分析类似的问题,对时频分析的结果产生不良影响。由于地面回波的特殊性,只有在频域上加窗才可以产生较好的时频聚集性。
PWVD公式定义为

(9)
式中:H(ξ)为频域的窗函数,作用是对WVD的频域平滑处理。
Mor-RPWVD时频分析首先计算引信差频信号的小波时频分布矩阵。为解决时频谱聚集、频率分辨率问题,引入Crazy Climbe提取小波时频分布的脊线,之后计算引信差频信号的PWVD分布。将两种时频分析矩阵进行融合,得到新的时频分析矩阵包含了所有的高低能量频率成分,融合的信息矩阵可以表示为
WMPS(tf)=SCAL(tf)+WPWVD(t,f)
(10)
重排方法通过重新安排在时频二维平面内的能量分布,有效改善了原始时频谱的能量分布,从而提高时频分辨率,并抑制交叉分量。重排可以表示为将在任何点(tf)处的值重新分配到(tf)点周围限定区域内能量重心(t)。
假定任意一点(tf)能量分布重心表示为
(11)
(12)
式中:h(·)为位置变量。
存在的信号频率成分经过重排后,在时频平面内能量得到积累,并同时能呈现出较好的时频分布效果。交叉分量经过重排后,在时频平面内能量基本保持不变。信号频率成分和交叉干扰项在时频平面内的差异性得到了放大,使得存在的频率分量在时频平面良好的展示出来。
为进一步提高Mor-RPWVD的交叉项干扰抑制能力和频率分辨率,引入距离加权的思想。传统的重排方法认为所有(tf)对于其重心(t)的影响相同,实际中(tf)距离点(t)越远,(t)点的能量值对原始点(tf)的影响越小,(t)加权时应该设定为较小权重系数。
重排到任意点(t)的值可由式(13)计算得到,它等于所有重排到该点的值之和:
(13)

Mor-RPWVD重新排列了融合时频分布矩阵,有效地提高了信号时频频谱的能量聚集性,保存了差频信号中的低能量频率成分,同时抑制了交叉项干扰,能够在较低全局阈值下得到较好的时频谱。
数据测试地点位于西藏羊八井地区,测试两种面目标为高寒干草地和高寒沼泽。两种面目标的主要差异体现在土壤含水量、地表植被、地表起伏等方面。测试示意图如图1所示,测试地点展示在图2中。引信信号频率为122 GHz,带宽为0.8 GHz,调制方式为锯齿波线性调频信号,调制频率为1.1 kHz,引信发射功率为1 mW。信号和地面之间的落角由一个3自由度云台控制。引信固定距离地面垂直高度为5 m。回波信号在接触地面时被地面反射。引信收到回波后进行混频处理,输出差频信号。计算机与引信的无线数据输出端相连,实时记录数据。

图1 数据测量示意图Fig.1 Data measurement diagram
为确保采集的数据不失一般性,在同一面目标随机选取3个不同的地点作为测试地点,每个地点测试的数据量为10 M数据,数据量较为充分。两种典型的面目标如图2所示。

图2 西藏地区典型面目标Fig.2 Typical area target
图3和图4展示了高寒干草地、高寒沼泽两种面目标引信测量的差频信号。

图3 高寒干草地引信差频信号Fig.3 Beat signal at alpine dry grassland

图4 高寒沼泽地引信差频信号Fig.4 Beat signal at alpine swamp
太赫兹引信的工作波长已经远远小于面目标的尺寸,根据电磁散射理论,面目标的散射特性已经属于准光学区。散射体各个部分之间的相互影响很小,散射几乎成为了一种局部现象而不再是积累的过程,表面电流积分的主要贡献来自于驻点和积分端点,面目标的散射也就可以认为是主要来自于这些为数不多的散射点,称为面目标的散射中心。面目标的回波信号特性则由多个散射中心决定,散射中心对于面目标散射特性的建模与识别有着重要作用。
几何绕射理论(GTD)模型是对面目标散射中心的经典描述,整个面目标散射场的近似式可以描述如下:
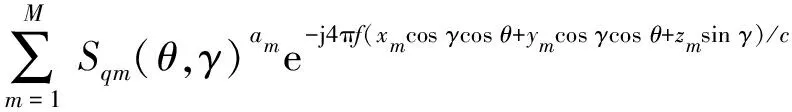
(14)
式中:Eq(f,θ,γ)为面目标散射场,q为特定的发射和接收极化组合,θ、γ分别表示散射中心的姿态角;
m为散射中心序号;
M为强散射中心数量,地面回波信号能量主要是来自于M个强散射中心;
Sqm(·)为第m个散射中心在中心频率f1上的散射系数因子;
am为中心类型参数;
(xm,ym,zm)表示散射中心的位置;
c为光速。
面目标总的散射场可以简化为
(15)
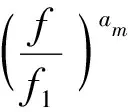

图5 锯齿波调频频率时间关系Fig.5 Sawtooth FM frequency-time relationship
发射信号频率表示为
(16)
fM为调制频率。
接收信号频率表示为
(17)
将fR(t)代入式(14),地面回波可以表示为

(18)
式中:rm可由下式计算:
rm=R0m+v0mt
(19)
R0m、v0m分别为匀速情况下第m个散射中心的初始距离和速度。记
aqm=Sqme-j4πf0/c
(20)
ωm=-j4πfR(t)rm/c
(21)
对于太赫兹引信,当带宽相同时具有更小的相对带宽。式(15)进一步简化可表示为
(22)
对于锯齿波线性调频体制,其面目标多散射点形成的回波,是以时间为变化量的多分量正弦信号组合模型,aqm、ωm代入式(18)中:
(23)

(24)
引信接收的地面回波信号是地面大量分辨单元后向散射中心电磁场矢量和。波束内地面散射体中心在空间和时间上都存在变化,进而影响的杂波幅度变化。因此,对地回波的幅值分布特性描述需要采用统计方法。
引信体制为锯齿波调频,引信发射信号st(t)可以表示为
(25)
式中:At表示信号幅度;
β=ΔFMfM表示信号调频斜率。
引信信号经过地面的后向散射,引信接收到的信号可以表示为式(24)。引信通过天线接收到的地面回波信号,经低噪放后,送至混频器与参考信号sl(t)混频。
sl(t)=Alst(t)
(26)
式中:Al为参考信号幅度。参考信号与面目标回波式(25)经过混频器后输出差频信号sl(t)。差频信号中包含的频率成分代表面目标的散射中心数量,也代表面目标的散射特性。差频信号sb(t)是引信进行面目标识别和引信炸高精准控制的基础,其表达式为
(27)


(28)
W(t,ω)进一步表示为
W(t,ω)=Wz(t,ω)+Wc(t,ω)
(29)
式中:Wz(t,ω)表示信号中存在的频率成分随时间的变化,
(30)
Wc(t,ω)表示多个频率成分存在的交叉频率分量。
回波信号中存在多个频率成分,每个频率成分的能量都受到散射系数因子Sqm的影响。Sqm是落角、频段、后向散射系数多种参量的函数,即使在单一周期内也存在着变化,造成信号能量随时间的变化,会给后续的频率提取增加困难。
太赫兹频段下面目标的回波不再是单点散射,而是典型的多点散射。引信落角通过影响后向散射系数进而影响面目标的散射特性。通过调整云台,调整引信的落角为65°、85°两种典型引信落角。利用小波时频、WVD、Mor-RPWVD分析方法对回波信号频率成分进行研究,进一步揭示面目标的多点散射特征。
4.1 高寒干草地85°落角下散射特性分析
首先对面目标(高寒干草地)引信差频信号进行分析。图6为高寒干草地在85°落角下利用3种时频分析方法对引信差频信号时频进行分析的结果。
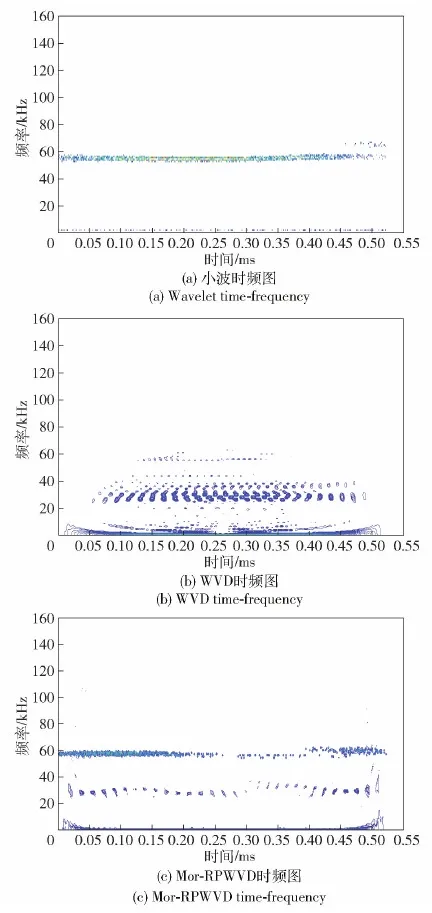
图6 85°落角下高寒干草地时频分析Fig.6 Alpine dry grassland time-frequency analysis under 85° fall angle
本文小波时频分析采用复Morlet小波。小波基带宽参数为4 Hz,小波的中心频率为4 Hz,频率分辨率为1.9 K,理论上可以完全区分差频信号中包含的两个不同频率成分。造成低频成分丢失的主要原因是有限的可利用数据长度问题。小波时频分析方法本质上依然是增加了窗函数来处理信号,并且没有充分利用数据的全周期特性。另一个原因是,回波中的两个频率成分能量不稳定,信号中的频率成分受到幅度调制,频率成分会出现不连续现象,进一步增加了频率分析的难度。WVD、Mor-RPWVD两种时频分析方法都提取出了差频信号中的两个频率成分,表明在85°落角下面目标(高寒干草地)为双点散射。WVD时频分析结果展示出了频率成分不连续、能量分布不均匀、严重交叉分量问题,提高了频率成分提取的难度,降低了频率分辨率。通过增加全局阈值的方法,限制交叉干扰项的同时也会限制存在频率成分在时频平面的表达。本文提出的Mor-RPWVD时频分析方法,在较小阈值下达到了良好的交叉分量抑制效果。提取出的两个频率成分为56.1 K和28.7 K。高频频率成分的能量聚集性高,取得了良好的时频分析效果。
4.2 高寒沼泽85°落角下散射特性分析
为了验证面目标(高寒干草地)双点散射分析结果,也为了验证Mor-RPWVD对面目标引信差频信号的分析效果,在另一个面目标(高寒沼泽)下进行相同条件下的测试,唯一变量为面目标的种类,其他实验参量不变,并对引信差频信号进行时频分析。图7为高寒沼泽85°落角下利用3种时频分析方法对引信差频信号时频进行分析的结果。

图7 85°落角下高寒沼泽地时频分析Fig.7 Alpine swamp time-frequency analysis under 85° fall angle
由图7可见:在此面目标(高寒沼泽)下,面目标散射特性为双点散射;
小波时频分析方法依然遗漏了低频信号成分;
WVD提取的频率成分出现了不连续、能量分布不均匀、严重交叉分量;
Mor-RPWVD时频分析方法得到的分析结果在抑制交叉分量、能量聚集性上都有良好的效果;
提取出的两个频率成分为57 K和27.3 K。
4.3 面目标65°落角下散射特性分析
为进一步研究不同引信落角下面目标的散射现象,改变引信的落角为65°,两种面目标下引信差频信号利用Mor-RPWVD时频分析结果展示如图8和图9所示。

图8 65°落角下高寒干草地Mor-RPWVD时频分析Fig.8 Alpine dry grassland Mor-RPWVD time-frequency analysis under 85° fall angle
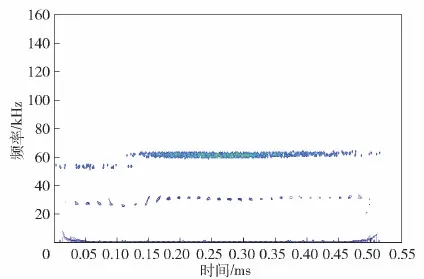
图9 65°落角下高寒沼泽Mor-RPWVD时频分析Fig.9 Alpine swamp Mor-RPWVD time-frequency analysis under 65° fall angle
由图8和图9可见:两种面目标落角65°条件下依然为双点散射;
Mor-RPWVD时频分析方法得到了较好的时频分析结果,验证了Mor-RPWVD对面目标差频信号突出分析能力;
高寒干草地两个频率成分为60.4 K和31.2 K;
高寒沼泽两个频率成分为61.3 K和30.7 K;
两种面目标的散射中心存在很小的差异。
本文采用小波时频、WVD、Mor-RPWVD分析方法研究了西藏地区两种典型面目标(高寒干草地和高寒沼泽)回波信号的时频特性,揭示了太赫兹引信经典落角65°、85°的面目标双点散射现象。基于GTD建立了太赫兹引信的回波模型,分析了多点散射面目标引信差频信号特性。利用WVD对差频信号的频率成分能量分布特性进行了分析。
小波时频方法分析差频信号丢失低频分量。WVD时频方法出现了较多的交叉分量,影响频率成分判断。利用Mor-RPWVD时频方法可以清晰地得出85°落角下面目标(高寒干草地)差频信号包含56.1 K和28.7 K两个频率成分,85°落角下面目标(高寒沼泽)差频信号包含57 K和27.3 K两个频率成分;
65°落角下面目标(高寒干草地)差频信号包含60.4 K和31.2 K两个频率成分,面目标(高寒沼泽)差频信号包含两个频率成分为61.3 K和30.7 K。分析数据发现,两种面目标的散射中心波动存在很小的差异。实测数据验证了Mor-RPWVD对面目标回波频率成分提取的优势。