刘一涵, 黄楷宸, 柏业超*
(1.南京大学 电子科学与工程学院,江苏 南京 210023;
2.南京大学 人工智能学院,江苏 南京 210023)
在武器装备试验获得大量的试验测量数据后,如何利用这些数据建立数学模型,分析测量数据误差并给出可靠的数据处理结果是武器装备系统和测控系统进行精度分析与鉴定的重要环节[1]。受外测设备测量环境、测量手段、测量元素等因素影响,且导弹飞行瞬态(如助推器脱落、级间点火和级间分离等)弹道特征点附近噪声相对较大、大量连续系统误差难以识别,使得外弹道测量数据误差复杂[2],随机误差大于测量的量化误差且存在非平稳时变特性,可模型化的误差带来了具有复杂特性和不确定性的模型误差,影响了数据处理精度。张峰等[3]采用样条函数建立了主动段运动模型,但是对于波动较大的弹道数据采用多项式或者样条函数描述弹道的方法不能保证轨道参数的逼近精度,会带来模型误差。李蝉等[4]提出了采用自适应抗差滤波方法实时计算再入弹道数据,该方法适用于非平稳测量数据处理,但是需要得到精确的测量数据和随机误差的统计特性,否则可能导致滤波发散,得到与实际情况相背离的结果。姚尚等[5]利用小波变换方法在时域和频域同时分析数据,根据分解的小波系数表现出的不同性质识别信号和噪声。李书兴[6]研究了经验模态分解(Empirical Mode Decomposition,EMD)方法在外弹道测量数据方面的应用,但是外弹道测量数据中不可避免地会带有各种噪声,特别是无线电测量设备受到环境电磁干扰时,采用EMD分析测量数据,经常出现模态混叠现象,导致分解后的本征模分量时-频分布混乱,失去实际物理意义。
本文提出了基于本征模态函数(Intrinsic Mode Function,IMF)能量拐点的外测数据误差分析方法。首先,采用EMD方法将外测数据分解成不同频率成分的本征模;
然后,根据外测数据随机误差、系统误差和真实数据的频率特征,采用IMF能量拐点方法将分解得到的IMF分成高频随机误差、混合信息和有效信息共3个集合;
接着将高频随机误差集合的本征模直接滤掉,对混合信息集合的IMF采用本文改进的反双曲正弦函数阈值函数作为调节因子进行小波滤噪,保留有效信息集合;
最后,分别采用小波重构和EMD重构得到滤掉随机误差的外测有效数据。本文方法综合利用了EMD和小波变换方法的优点,避免了单一使用一种方法的局限,有效地分离了低频和次低频误差,避免了非平稳测量数据近似成平稳测量数据处理过程中引入的模型误差,适合非线性、多频段测量数据误差分析。
外测测量设备包括各式雷达和光电经纬仪等。这些设备的测量元件可分为单脉冲雷达、相控阵雷达、红外传感器和可见光传感器等,测量元素主要有距离、角度、速度,测量平台有固定站、车载平台、舰载平台等,因而设备误差也是复杂多样的。其复杂性不仅表现在不同的测量体制间,也表现在同一测量体制、不同测量手段的测量数据,例如多传感器光电经纬仪,虽然中波红外传感器和可见光传感器都是光学测量,但是由于安装的位置和成像的原理等不同,测量数据误差特性也不相同。但是即使采用同一测量手段,不同时间进场的测量设备其数据误差表现也不尽相同。外测数据随机误差具有不可观测性、强相关性和非平稳时变特性。从工程技术来看,随机误差有时大于测量的量化误差。从测量时间段看,各个时间区域方差大小是有变化的。系统误差只有部分可以通过标校测定和修正,这样的系统误差数值较大,即使实际上可以建模的系统误差采用最可靠的误差修正模型,在弹道不同测量弧段也存在着不同的误差修正残余量,还有些系统误差不能标校或者不能建立修正模型,这些系统误差往往具有潜伏性,不易识别,很难与随机误差分离。
文献[1]定义了外测测量数据的数学模型:
y(t)=f(t)+s(t)+e(t)
(1)
式中:y(t)为测量数据;
f(t)为真实数据;
s(t)为系统误差;
e(t)为随机误差。系统误差反映了测量数据的准确度,随机误差反映了测量数据的精密度。要获得高精度的数据,必须准确地分离系统误差和随机误差。
文献[2]根据外测数据在不同的频带中都具有能谱分布,测量数据系统误差一般可分为常值误差、线性漂移误差、周期性误差和复杂规律变化误差等,因此定义测量数据模型为
y(t)=P(t)+B(t)+ε(t)
(2)
式中:y(t)为测量数据;
P(t)为真实数据;
B(t)为漂移误差;
ε(t)为随机误差。B(t)中所含的频率成分比真实数据P(t)快,但与随机误差ε(t)相比要慢,因此又可称为次低频误差。
2.1 外测数据3个集合{fIMF(i)}与{E(i)}的能量关系
文献[2]根据大量实例认为式(2)中P(t)和B(t)之间、B(t)和ε(t)之间通常都存在一个频带间隔,提出三频带信号分离的样条函数方法[2]。该方法分析非平稳数据会因所选的节点数目、位置和待估参数的增多而导致信号估计的精度不高。
EMD的基本思想为将一个频率不规则的波转换为多个单一频率的波+残波的形式[7-9]。
EMD算法采用“筛分”的方法将IMF层层筛选出来,将外弹道测量数据分解成不同时间尺度的IMF和一个残差信号之和,详细步骤如文献[6]所示。
外弹道测量数据经EMD后得到n个IMF,各个IMF分量记作{fIMF(i)},{fIMF(i)}的能量{E(i)}的计算公式为
(3)
外测数据序列的总能量记为E0,其计算公式为
(4)
对各层{fIMF(i)}能量{E(i)}归一化处理,其计算公式为
(5)
文献[2]从理论上证明了式(2)中P(t)与B(t)有分频界点、P(t)+B(t)与ε(t)有分频界点并且采用分频方法对运载火箭的外弹道跟踪测量信号进行分析处理,成功地分离了测量信号中的轨道、漂移误差和随机误差[2]。
根据外测数据特点和测量数据的数学模型以及文献[2],根据IMF能量集合{E(i)},将外测数据EMD后得到的{fIMF(i)}划分为高频随机误差集合A、混合信息集合B和有效信息集合(含有低频的系统误差和真实数据)C,即
A={fIMF(i),i=1,…,m-1}
B={fIMF(i),i=m,…,p-1}
C={fIMF(i),i=p,…,n}
集合A含有高频的随机误差,其{fIMF(i)}随着分解层数的增加,高频随机误差成分减少,因此fIMF(i)的能量逐渐降低。
集合B含有较高频的真实数据,部分次高频和较高频的系统误差、次高频和较高频随机误差,其{fIMF(i)}随着分解层数的增加,频率成分增加。
划分能量拐点的准则为
if((EIMF(i+1)-EIMF(i))>0&(EIMF(i+2)-EIMF(i+1))<0),
k=i+1
(6)
2.2 基于IMF能量拐点的测量数据成分集合判断算法
基于IMF能量拐点的测量数据成分集合判断的具体算法如下。
① 输入外弹道测量序列x(t),i=1。
② 对x(t)进行 EMD分解,得到不同的{fIMF(i)}。
③ 根据式(3)计算各分量的能量Ei。
④ 根据式(5)计算各分量归一化能量εi。
⑤ 计算相邻分量的能量差,即δ=εi+εi-1。
⑥ 按式(6)寻找分量能量拐点。
2.3 混合信息集合的处理
基于改进的EMD和小波变换滤噪算法思想是对测量数据{x(t)}(t=1,2,…,N)进行EMD,采用本文的能量拐点计算方法判定3个集合的临界点,将高频噪声集合直接滤除,有效信息集合保留,混合信息采用db4小波分解,根据各层小波系数的标准方差确定滤噪阈值。
采用db4小波对混合信息集合和有限信息集合的各{fIMF(i)}进行分解,一般分解层数为3或4层即可,具体分解过程见文献[3]。设{fIMF(i)}k时刻在第j层的低频系数为ai,k、高频系数为di,k[10]。
混合信息中噪声和有效数据没有明确的界限,采用硬阈值函数和软阈值函数滤噪时,若将绝对值比设定阈值大的小波系数直接置为0[11],会删除掉一些有用的信息,从而降低信号重构后的精度[12]。本文采用反双曲正弦函数作为阈值函数的调节因子。
(7)
因此本文的阈值函数为
(8)
(9)
式中:σj为第j层小波系数的标准方差。
sinh是奇函数且关于原点对称,值域区间为(-∞,∞),是在定义域区间内非线性单调上升的连续函数。采用反双曲正弦函数作为阈值函数调节因子,则当|dj|=Tj时,Dj=0,Dj连续;
当|dj|→∞时,Dj=|dj|。其克服了硬阈值函数Gibbs振荡现象,也解决了软阈值函数当|dj|→∞时Dj存在的与Tj的固定偏差[13-14],其估计的小波系数小于真实的小波系数绝对值,导致重构后的信号出现细节缺陷问题。
3个集合的处理算法如下。
① 对x(t)进行EMD。
② 判定高频噪声集合、混合信息集合和有效信息集合。
③ 对混合信息集合的m~p-1的fIMF(i)进行db4小波变换。
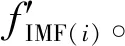
⑥ 有效信息与x1(t)重构后得到去噪后的有效外测数据。
3.1 分析案例
以某舰载雷达的一次测量数据为例进行分析。雷达固连在船上,测量平台受海况和船的航行状况影响,测量平台有颠簸、摇摆、振动和航行等复杂运动,测量数据是误差成分复杂的非平稳测量序列。
将北斗测量数据经坐标转换得到待分析舰载雷达测量数据真值[15-16],将真值和实际测量数据作差,得到残差数据,此时残差数据包括测量数据的随机误差和系统误差。然后采用表1中4种方法分离残差数据中系统误差和随机误差。

表1 实验方法
按照表1的4种方法,分离了随机误差和系统误差,用滤掉随机误差的测量数据计算目标弹道轨迹,并用与北斗定位结果的弹道差异来分析方法的有效性。
采用本文方法结合方位角残差数据说明具体分析过程。
图1为方位角残差数据图。图1中数据起伏较大,说明数据随机性强,显然是非平稳数据,若视为平稳数据滤波,必然会影响数据精度。

图1 方位角残差数据图
图2为IMF1~IMF9及其频谱图。从图2可以看出,由残差数据经EMD得到的IMF在时域上特点不同,看不到与时间有关的周期性成分存在。IMF1 存在很多高频信号,且幅值较大。IMF2信号主要集中在频段0.7~1.8 MHz。IMF1~IMF4低频分量较多,表现为低频信号。IMF5~IMF9频谱中低频分量的幅值远高于高频分量的幅值。IMF8和IMF9可以视作没有高频分量,相较于IMF7低频幅值更大。
图3为IMF1~IMF9时域振幅图。显然IMF8和IMF9振幅较大,余下的IMF振幅在时域上很难分辨。图4为IMF1~IMF9频域幅度图。IMF信号从高频到低频排列,IMF4、IMF7和IMF8呈现明显的周期性。
将分解得到的IMF系数代入式(3)和式(5),计算各层IMF的能量和能量变化,如表2所示,归一化的各层IMF的能量和EMD分解层数,如图5所示。
如果残差数据为白噪声数据则经EMD会从第2个IMF开始,IMF能量呈线性关系,从图5可以看出,残差数据不是白噪声数据。分解层数为4和7时是能量曲线的拐点,这与表2中δ4<0,δ7<0,一致,显然IMF4和IMF7为能量拐点。

图2 IMF1~IMF9及其频谱图
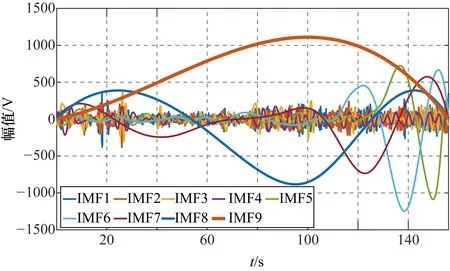
图3 IMF1~IMF9时域振幅

图4 IMF1~IMF9频域幅度图
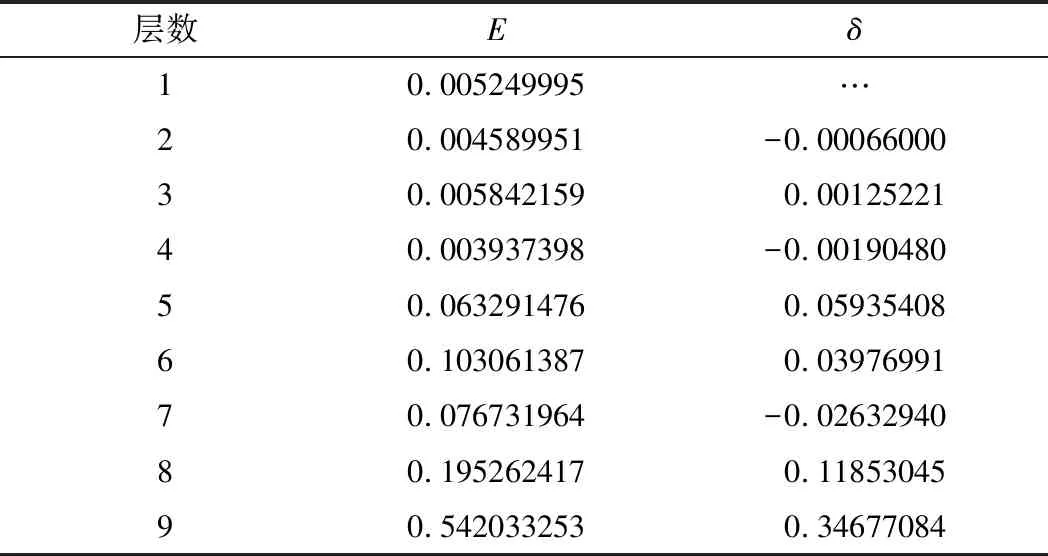
表2 IMF能量和能量变化
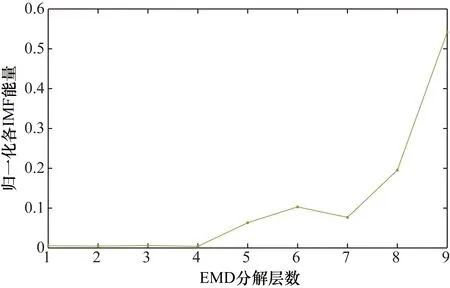
图5 IMF能量和EMD分解层数图
高频随机误差集合={IMF1,IMF2,IMF3,IMF4},混合集合={IMF5,IMF6,IMF7},有效集合={IMF8,IMF9}。
有效信息集合是低频和次低频的系统误差。
对混合信息集合的混合信息集合元素采用本文新的阈值函数由式(7)~式(9)计算,分别小波滤噪,经重构后得到滤噪后的混合信息和混合信息中的随机误差,然后将混合信息的随机误差与高频随机误差集合元素重构得到了该测量数据的随机误差序列。混合信息滤噪后进行重构得到了混合信息中的系统误差,并与其有效信息集合的元素重构数据相加得到测量数据的系统误差序列。
3.2 4种方法得到的结果分析
4种方法分离得到的系统误差和随机误差如图6所示。
从图6(a)、图6(b)和图6(d)中的系统误差和随机误差界限分明,系统误差数值明显小于随机误差,图6(c)中系统误差和随机误差混叠,系统误差数值小于随机误差,图6(d)中系统误差曲线光顺,系统误差和随机误差没有混叠。
采用4种方法分离系统误差和随机误差后,用测量数据补偿系统误差,计算目标弹道轨迹,得到与北斗定位结果的弹道差别均方根,如表3所示。

表3 弹道差别表 单位:m
从表3可以看出,本文方法与3个方法相比,在X、Y、Z轴3个方向精度都有所提高。X方向方法4、方法3、方法2的误差分别是本文方法的1.59倍、1.28倍、1.09倍;
Y方向方法4、方法3、方法2的误差分别是本文方法的1.52倍、1.24、1.09倍;
Z方向方法4、方法3、方法2的误差分别是本文方法的1.52倍、1.30倍、1.06倍。显然将本文方法分离得到的系统误差补偿到测量数据,计算得到的弹道轨迹与真值差别最小、精度最高,特别是23.7 s数据,方法3和方法4分离的结果是估高了随机误差影响,降低了系统误差估值,系统误差补偿不够,导致计算的坐标与真值坐标差值很大,方法2分离的结果是估高了系统误差数值,方法1分离的结果是系统误差和随机误差共同作用引起残差数据跳变,对测量数据补偿的系统误差值最合理,因此与真值弹道差别最小。
外测数据误差分析是外弹道参数处理的关键环节,利用基于IMF能量拐点的测量数据成分集合判断方法和基于反双曲正弦函数调节的小波去噪方法,有效地分离了测量数据的系统误差和随机误差。经数据验证,相比较本文新定义的阈值函数小波滤噪、EMD滤噪和多项式滤噪方法,本文方法与真值弹道差别最小,提高了定位精度。但是混合信息的小波滤噪如何设置最优阈值需要进一步解决。

图6 4种方法分离得到的系统误差和随机误差
猜你喜欢系统误差弹道阈值弹道——打胜仗的奥秘小哥白尼(趣味科学)(2022年3期)2022-06-09小波阈值去噪在深小孔钻削声发射信号处理中的应用制造技术与机床(2019年9期)2019-09-10一维弹道修正弹无线通信系统研制电子制作(2019年7期)2019-04-25基于自适应阈值和连通域的隧道裂缝提取西南交通大学学报(2018年6期)2018-12-18基于ADS-B的航空器测高系统误差评估方法北京航空航天大学学报(2017年4期)2017-11-23比值遥感蚀变信息提取及阈值确定(插图)河北遥感(2017年2期)2017-08-07基于Bagging模型的惯导系统误差抑制方法中国惯性技术学报(2017年1期)2017-06-09存在系统误差下交叉定位系统最优交会角研究系统工程与电子技术(2016年7期)2016-08-21室内表面平均氡析出率阈值探讨衡阳师范学院学报(2016年3期)2016-07-10基于PID控制的二维弹道修正弹仿真制导与引信(2016年3期)2016-03-20