熊 峰,李宗春,付永健,何 华
(信息工程大学 地理空间信息学院,郑州 450001)
随着智慧城市、建筑信息模型(building information modeling, BIM)、城市信息模型(city information modeling, CIM)等概念的提出和空间数据获取技术的深度发展,准确高效地重建城市三维模型,从而实现三维现实世界的准确理解和精细表达逐渐成为当下的发展趋势和研究热点[1-3]。建筑物作为城市场景中的主要构成成分,建筑物几何模型的重建研究得到了广泛的关注和发展[4]。
地面激光扫描(terrestrial laser scanning, TLS)系统是建筑物模型重建中数据获取的重要来源,能快速采集包含大量细节特征(如门窗等)的建筑物立面点云数据,从而对机载建筑点云进行有效的补充和扩展[4-5]。建筑物立面结构线的自动获取不仅能简化建筑物的形状结构和复杂的拓扑关系,而且可用于建筑物立面重建等工作中。因此,有效挖掘并提取建筑物立面结构线具有十分重要的意义。
按照文献[6]的定义,建筑物结构线可分为边界线和折叠线,如图1所示。结构线提取的关键在于对属于边界线和折叠线上的特征点进行判断和定位,文中主要针对边界特征点进行探讨和研究。目前,国内外学者针对建筑物立面边界特征点提取已展开了大量研究,现有的提取方法大致可归纳为三类:①基于图像的方法[7-10]。通常是将三维点云转换成二维图像,然后应用图像处理的方法检测边界特征点。该方法虽可以充分利用图像领域中成熟的边界提取技术,但在转换过程中易丢失三维信息,存在一定的精度损失。②基于平面的方法[11-14]。此类方法先将建筑物点云数据分割为不同的平面,再提取每个平面的边界点,从而实现边界特征点的提取。该方法在平面特征显著的情况下提取结果较好,但其倾向于拟合成较大平面,容易丢失较多的细节。③基于点的方法[15-18]。一般是通过局部特征直接从原始建筑物点云数据中提取边界特征点。该方法能充分挖掘特征点的几何拓扑关系,但抗噪性差,提取结果十分依赖局部特征的选取。

图1 建筑物立面结构线示意图
凸包(Convex Hull)[19]自提出以来被广泛用于不同数据的边界点提取。在建筑物边界特征点提取方面,Sampath等[20]改进了凸包算法,首先选择点云数据的坐标极值点为初始边界点,然后依次求解各点邻域内与某一方向夹角最大或最小的点作为下一个边界点,直至提取出机载点云中建筑物外边界特征点,但无法提取出内边界特征点,且一次仅能处理单一建筑物点云数据;
庞世燕等[12]在提取出建筑物立面点云中的平面特征的前提下,通过构建三角网将三角形连接数较少的点作为候选边界点来提高凸包算法提取边界特征点的速度和稳定性,但其仍不能直接提取立面内边界特征点。Tseng等[21]首先提取出机载建筑物点云,然后进行分割处理,再利用文献[20]中改进的凸包算法提取出边界特征点,但依旧无法处理建筑物点云内部存在孔洞的情况。对此,文中针对现有算法较难提取出建筑物立面点云中的边界特征点、提取效果差等问题,提出一种构建凸包三角网的建筑物立面边界特征点提取方法,首先对各点及其近邻点进行投影与坐标转换,然后利用凸包算法初步提取边界特征点后,对剩余点的凸包建立三角网,统计近邻点在各三角形中的占比率以及各三角形的顶角大小,以此来筛选出建筑物立面点云中其余边界特征点。
由于点云数据中各点之间不具备空间拓扑关系,对任一目标点是否为边界特征点的判定可以依据该目标点的近邻点几何特性来判定[6]。文中通过分析边界特征点与非边界特征点之间的邻域几何拓扑差别,借助凸包算法等理论提出一种新的边界特征点提取方法,具体技术路线如图2所示。
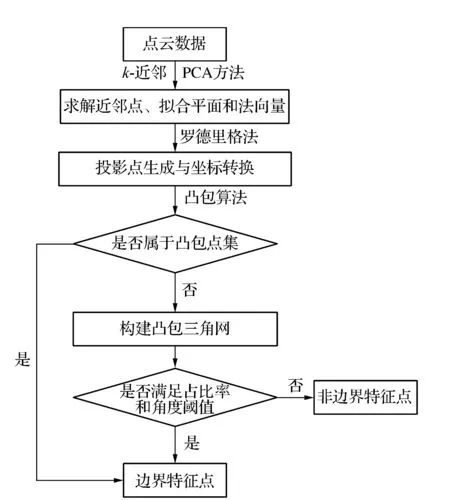
图2 文中方法技术路线
1.1 近邻点投影与坐标转换
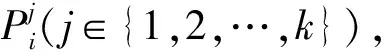
(1)
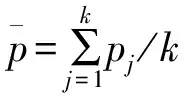

(2)
(3)
经过上述步骤,获得了目标点O0在拟合平面的近邻投影点。随后,选用基于罗德里格旋转公式将三维平面旋转至与xoy平面平行。主要步骤如下:
Step1:依据目标点法向量n0与xoy平面法向量nz=(0,0,1)计算旋转角φ及旋转轴l。
(4)
Step2:基于旋转角φ和旋转轴l=(p,q,t)按照罗德里格公式求解旋转矩阵R。
(5)
Step3:左乘旋转矩阵得到平行于xoy面的近邻投影点
(6)
近邻点投影与坐标转换过程如图3所示。

图3 近邻点投影与坐标转换示意图
1.2 边界特征点提取
二维凸包是几何计算中普遍采用的一种结构计算办法,若平面上存在有限个点的点集S,其凸包是包含S的最小凸多边形[22]。在1.1节中,已将各点的近邻点转换为平面点集,在此基础上,用凸包思想分析各点的邻域几何拓扑关系,可以发现:在理想情况下,边界特征点呈连续的直线分布,以近邻点数k=12为例,绘制的边界特征点及内点(非边界特征点)的凸包如图4所示,利用边界特征点的近邻点所求得的凸包点集包含该边界特征点,而内点的凸包点集不会包含该内点。在实际的数据采集过程中,获取的点云数据不均匀,其边界特征点往往是紊乱的,潜在边界特征点及内点(非潜在边界特征点)的凸包如图5所示,利用潜在边界特征点的近邻点所求得的凸包点集难以包含该潜在边界特征点,且内点的凸包点集仍不会包含该内点。

图4 理想情况下的凸包求解示意图

图5 一般情况下的凸包求解示意图
但潜在边界特征点靠近附近边界特征点,其近邻点分布仍具有偏向一侧的特性,且与附近边界特征点的连线间存在一个较大的夹角。如图6所示,潜在边界特征点O与附近边界特征点A和特征点B连线间的夹角,比内点O′与附近边界特征点C和特征点D连线之间的夹角大一些。
因此,为尽可能提取出能描述边界特性的潜在边界特征点,文中以目标点为中心,构建凸包三角网(在图5的基础上构建的凸包三角网如图6所示),通过定义三角网中近邻点在各三角形中的占比率δm(m为三角形编号)和以目标点为顶点的三角形的顶角值φm来描述潜在边界特征点的特性,即潜在边界特征点越靠近附近边界特征点,其近邻点在三角形中的δm越低,且φm越大。
(7)
式中:k为目标点的近邻点数量;
tm为近邻点在编号为m的三角形中的数量。
综上所述,文中提取边界特征点的主要步骤如下:
Step1:求解各点的近邻点集并进行投影和坐标转换,基于凸包算法[23]求解各点的近邻点经投影及坐标转换后的凸包点集。若目标点属于该点集,则该点为边界特征点,否则构建凸包三角网进一步予以判断。
Step2:在Step1的基础上,计算各三角形中近邻点占比率δm,并统计各三角形的顶角值φm。
Step3:若各三角网的δm均大于占比率阈值δ0(见图6),则认为该点的近邻点均匀分布在该目标点附近,直接判定该点为内点(如图6(b)所示内点凸包三角网,设置较小的δ0时各三角形中近邻点占比率);
对小于占比率阈值δ0的三角形统计得到最大顶角值φp(如图6(a)所示潜在边界特征点的凸包三角网,当存在①号和②号等多个三角形占比率均小于阈值δ0,采用最大顶角值进行下一步筛选),如果φp大于等于角度阈值φ0,则认为该点为边界特征点,否则为非边界特征点。
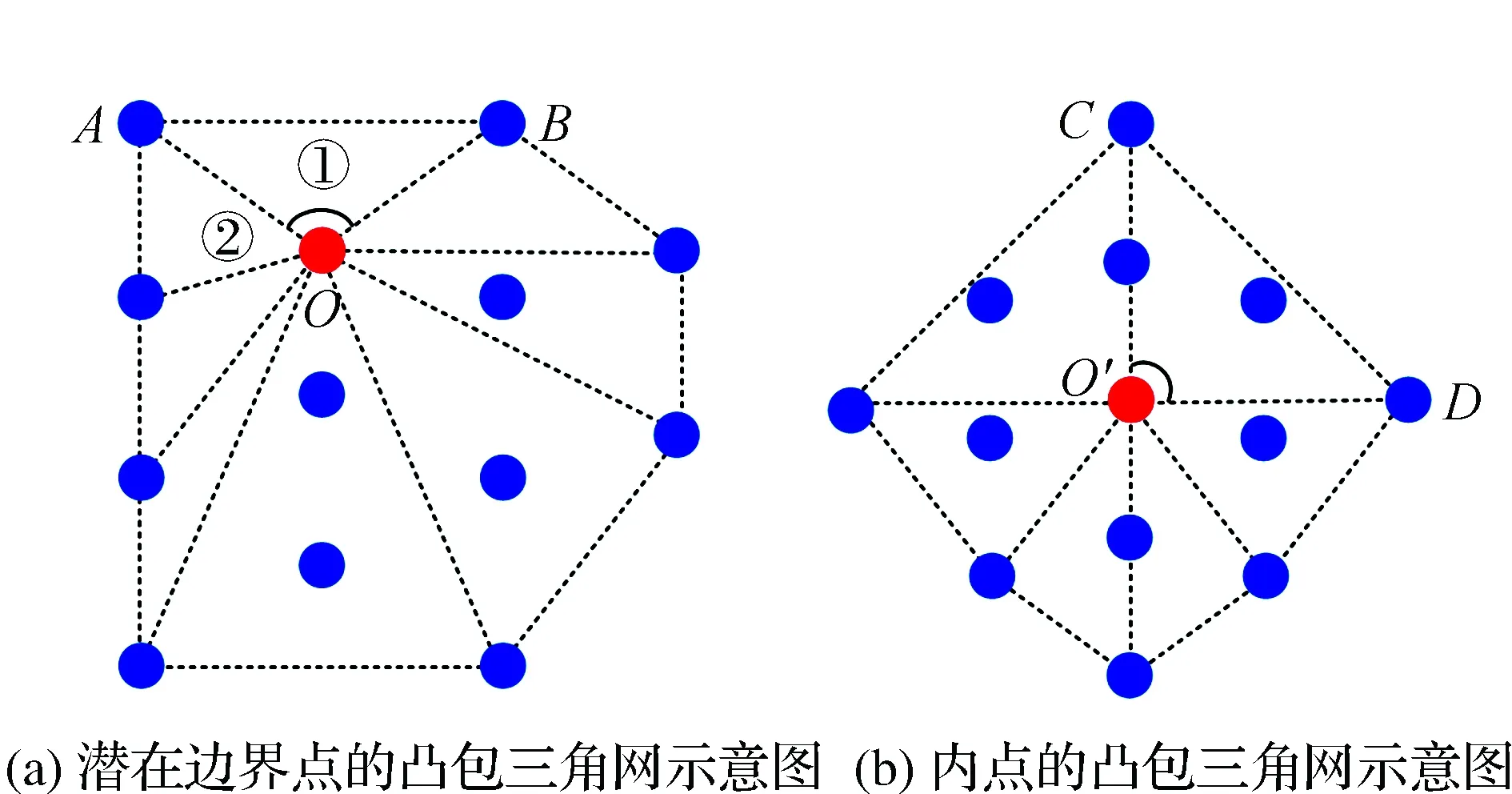
图6 一般情况下的凸包三角网构建示意图
2.1 试验平台与数据
试验均在Intel(R) Core(TM)i7-8700 CPU @ 3.20GHz RAM 8GB的计算机上展开。选取一组模型采样点云数据及四组实测点云数据以验证方法的有效性,其中,Data1、Data2、Data4数据是使用Riegl VZ-400地面激光扫描仪在某学校校园采集得到的局部建筑物立面点云数据;
Data3数据是参考文献[24]中的方法通过构建建筑物立面BIM模型生成的点云数据,数据分布情况较为理想;
Data5数据是从开源数据集Robotic 3D Scan Repsitory-12中选取的某一建筑物立面数据,该立面存在较多不规则局部凸起,数据分布情况较为复杂。5组试验数据相关信息如表1所示。
表1 试验数据相关信息
2.2 评价指标
为定量评价文中方法的性能,采用简化率(simplification rate, SR)以及精度P、召回率R和F1得分4个指标对建筑物立面边界特征点提取结果进行评价,具体计算方法见式(8)。
(8)
式中:NB为文中方法提取的建筑物立面边界特征点数量;
N0为文中建筑物立面点云总数;
TP为文中方法正确提取的建筑物立面边界特征点数量;
FP为文中方法错误提取的建筑物立面边界特征点数量;
FN为文中方法未提取出的建筑物立面边界特征点数量。
2.3 参数设置
利用文中方法从试验数据中提取建筑物立面边界特征点,涉及的参数主要有近邻点数量k、三角网中近邻点的占比率阈值δ0、角度阈值φ0。近邻点数量k是用来定义每个目标点的近邻点个数的参数;
占比率阈值δ0是用来判断是否为边界特征点的重要指标,用于描述目标点的近邻点集的分布情况,即潜在边界点越靠近附近边界特征点,该三角网中的近邻点越少,对应的占比率越低,因此,阈值一般选择较小值;
角度阈值φ0是在满足占比率阈值δ0的前提下进一步筛选的参数,角度越大,说明越靠近附近边界特征点,即可能是潜在边界特征点。表2为文中5组试验对应的参数设置,其中,Data1、Data2数据较为理想,对应的参数设置是在已知真值的前提下依据评价指标获得的,其他数据的参数设置均为目测较好的试验结果对应的参数。
2.4 定量试验
为验证和评价文中方法的性能,利用Data1和Data2实测点云数据进行试验。两组点云数据分布较为规则,以人工提取最外侧的边界特征点作为真值。引入文献[20]中改进的凸包算法、文献[17]中基于点的边界特征点提取方法与文中方法进行对比分析,文献[20]中通过改进凸包算法,逐点判断当前点与近邻点的连线和某一固定方向之间的夹角来寻找边界特征点,文献[17]中针对边界特征点提出了一种简单有效的检测方法,即通过计算每个点的近邻点集的重心点到当前点的距离来判定是否为边界特征点。表3统计了文献[20]、文献[17]方法和文中方法对两组点云数据的边界特征点提取前后的点云数量、简化率SR、精度P、召回率R和F1得分,提取效果如图7和图8所示。

表2 文中方法试验参数设置

表3 两种点云数据定量评价结果

图7 Data1提取结果

图8 Data2提取结果
综合分析表3和图7~8,可以发现:
1) Data1、Data2分别为曲面和平面类型点云数据,3种方法均能提取出两种立面形状的边界特征点,但文献[20]方法无法提取出立面内边界特征点(如图8(c)椭圆圈所示),另外,由于拐角处边界特征点(如图8(d)圆圈中的拐角处)的重心点与特征点之间的距离相较于其他特征点小一些,文献[17]方法难以很好地提取出拐角处边界特征点。
2)3种方法均具有较高的简化率,能使原始点云数据得到很好简化。结合F1得分指标来看,文中方法在简化数据的同时,能较好地保留边界特征信息,达到更好的提取效果。需要说明的是,文献[20]方法在Data2中的简化率较高的原因在于该方法漏提取了内边界特征点;
3)文中方法在精度、召回率和F1得分3个指标的综合表现上优于文献[20]和文献[17]方法,提取结果与人工提取的边界特征点达到了很高的吻合度,可以提取出较为显著的边界特征点。但文中方法需要逐点判断,无法与文献[17]方法一样实现批量处理,因此较耗时。
2.5 对比试验
为进一步展示建筑物立面边界特征点提取效果,分别采用文献[20]、文献[17]方法以及文中方法对Data3、Data4、Data5进行边界特征点提取,提取结果如图9~11所示。

图9 Data3提取结果对比

图10 Data4提取结果对比

图11 Data5提取结果对比
由图9~11的提取结果可知,文献[20]方法仅能提取出建筑立面的外边界特征点,而文中方法与文献[17]方法均能对建筑立面内外边界特征点进行有效提取,可以较直观地反映出建筑物立面的形状结构,其中,Data3、Data4的边界特征点提取效果相当,但对于Data5,文献[17]方法漏提取或误提取现象较为严重,如图11(c)所示,提取的边界特征点明显存在边界缺失或局部误提取的现象,而文中方法提取结果较为完整,提取出的边界特征点较为准确。分析其原因主要是,文献[17]基于距离指标的判断方法更适用于点云规则分布的平面边界特征点的检测,对于点云密度差异明显的建筑物立面难以设置合适的距离阈值,因此容易出现边界缺失或局部误提取的现象;
而文中方法对近邻点进行了坐标投影和转换操作且采用占比率和角度指标,受局部凸起和点云密度不一的影响更小一些。
文中针对建筑物立面重建的现实需求,以地面LiDAR点云数据为研究对象,基于传统的凸包算法,提出了一种用于建筑物立面边界特征点提取的凸包三角网方法。选取模型采样点云数据及不同类型、不同密度的实测建筑立面点云数据进行试验,结果表明,文中方法能有效提取出建筑立面边界特征点,较好地保留了特征信息,并且不易受立面类型不同和点云密度变化的影响,具有较强的适应性,可为建筑物结构线的提取以及建筑物立面建模提供前期保障。但所提方法需要逐点判断、较为耗时,下一步将继续优化方法,降低时间成本。
猜你喜欢内点三角网边界拓展阅读的边界儿童时代·幸福宝宝(2021年11期)2021-12-21意大利边界穿越之家现代装饰(2020年4期)2020-05-20结合Delaunay三角网的自适应多尺度图像重叠域配准方法软件导刊(2020年11期)2020-01-05论中立的帮助行为之可罚边界证券法律评论(2018年0期)2018-08-31针对路面建模的Delaunay三角网格分治算法智能计算机与应用(2017年2期)2017-05-04基于罚函数内点法的泄露积分型回声状态网的参数优化自动化学报(2017年7期)2017-04-18基于内点方法的DSD算法与列生成算法湖南城市学院学报(自然科学版)(2016年4期)2016-02-27一个新的求解半正定规划问题的原始对偶内点算法应用数学与计算数学学报(2014年3期)2014-09-26“伪翻译”:“翻译”之边界行走者外语学刊(2014年6期)2014-04-18基于内点法和离散粒子群算法的输电网参数辨识电力工程技术(2014年1期)2014-03-20