朱军伟, 顾丽娜, 李生彪
(1.杨凌职业技术学院, 陕西 杨凌 712100;
2.兰州文理学院, 兰州 730000)
近年来,学者们对Sturm -Liouville有限谱问题进行了较多研究[1-7],但对于奇数阶具有有限谱的微分方程边值问题研究得较少.2013年, Ao等[8]讨论了一类边界条件带有谱参数且具有转移条件的正则Sturm -Liouville问题的特征值数量.2017年, Ao[9]研究了如下两类三阶边值问题:
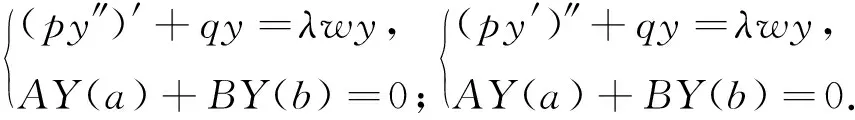
研究显示,对于每一个正整数m, 上述问题至多有2m+1个特征值.受上述文献启发,本文对如下转移条件下边界中含有谱参数的两类三阶边值问题进行研究:
(1)
(2)

r=1/p,q,w∈L(J,C),
(3)
其中L(J,C)为Lebesgue可积的复值函数在J上构成的集合.
令u1=y,u2=y′,u3=py″, 则与方程(py″)′+qy=λwy等价的系统可表示为:
u′1=u2,u′2=ru3,u′3=(λw-q)u1.
(4)
定义1设y=y(t)为问题的解.若y≡0,u2=y′≡0,u3=py″≡0, 则称y为问题的平凡解,反之称为非平凡解.
引理1设Φ(x,λ)=[φij(x,λ)]是系统(4)满足初始条件Φ(a,λ)=I的基解矩阵,则λ∈C是式(1)的特征值当且仅当
Δ(λ)=det[Aλ+BλΦ(b,λ)].
(5)
特别地
(6)
其中:
h11(λ)=-(λβ′1+β1)(λα′2-α2+λα′3+α3),h12(λ)=(λβ′1+β1)(λα′3+α3-λα′1+α1),
h13(λ)=-(λβ′1+β1)(λα′2+α2-λα′1+α1),h21(λ)=(λβ′2+β2)(λα′3+α3+λα′2-α2),
h22(λ)=(λβ′2+β2)(λα′1-α1-λα′3-α3),h23(λ)=-(λβ′2+β2)(λα′2-α2+λα′1-α1),
h31(λ)=-(λβ′3-β3)(λα′2-α2+λα′3+α3),h32(λ)=(λβ′3-β3)(λα′3+α3-λα′1+α1),
h33(λ)=(λβ′3-β3)(λα′1-α1-λα′2-α2).
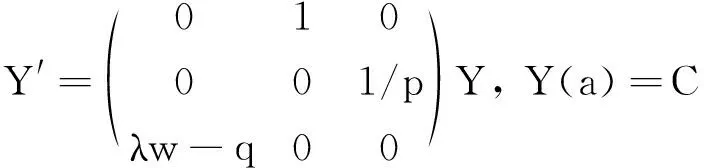

首先假设J=(a,c)∪(c,b)存在如下划分:
(7)
(8)
当q(t)=w(t)=0时有:
(9)
为便于后续计算,在式(7)—(9)的基础上本文补充如下相关条件:
(10)
引理2令Φ(t,λ)=[φij(t,λ)]是系统(4)满足初始条件Φ(a,λ)=I的基解矩阵,则有
(11)

(12)
其中:φ11(a3,λ)=(a3-a1)r0(λw0-q0)+1,φ12(a3,λ)=(a3-a1)[r0(λw0-q0)(a1-a0)+1]+(a1-a0),φ31(a3,λ)=[(a3-a1)r0(λw0-q0)+1](λw1-q1)+(λw0-q0),φ32(a3,λ)=(λw1-q1)(a3-a1)r0+1.当1≤i≤m时有:
(13)
证明由式(4)可知,在r恒等于零的子区间上u2是常数,在q和w恒等于零的子区间上u3是常数.于是根据Φ(a1,λ)和Φ(a3,λ)以及式(4)即可递推出引理2中Φ(a2i+1,λ)的结构,引理2得证.
引理3令Ψ(t,λ)=[ψij(t,λ)]是系统(4)满足初始条件Ψ(c,λ)=I的基解矩阵,则有
(14)
(15)

(16)
证明由于证明方法与引理2的证明方法相同,故本文在此省略.
引理4令Φ(t,λ)=[φij(t,λ)]是系统(4)满足初始条件Φ(a,λ)=I的基解矩阵,且Ψ(t,λ)=[ψij(t,λ)]与引理3中给出的意义一致,则有
Φ(b,λ)=Ψ(b,λ)GΦ(c,λ),
(17)
其中G=[gij]3 ×3=-D-1C,Ψ(c-,λ)为Ψ(c,λ)在c点处的左极限.
证明由转移条件可知CΦ(c-,λ)+DΦ(c+,λ)=0, 从而有Φ(c+,λ)=-D-1CΦ(c-,λ)=GΦ(c-,λ).注意到Φ(c,λ)=Φ(c-,λ)=Φ(a2m +1,λ),Ψ(b,λ)=Φ(b2n +1,λ),Φ(c-,λ)=I, 故由引理2和引理3得Φ(b,λ)=Ψ(b,λ)GΦ(c,λ), 其中Ψ(b,λ)=Φ(b2n +1,λ).证毕.
引理5令Φ(t,λ)=[φij(t,λ)]是系统(4)满足初始条件Φ(a,λ)=I的基解矩阵,则对于每一个λ∈C,Φ(b,λ)有:

证明由引理1可知:
其中:
θ11=1+rm -1(λwm -1-qm -1)=rm -1(λwm -1-qm -1)+o(λwm -1-qm -1),
θ12=2+rm -1(λwm -1-qm -1)=rm -1(λwm -1-qm -1)+o(λwm -1-qm -1),
θ13=2rm -2+rm -1rm -2(λwm -1-qm -1)=rm -1rm -2(λwm -1-qm -1)+o(rm -1rm -2(λwm -1-qm -1)),
θ21=rm -1(λwm -1-qm -1)=rm -1(λwm -1-qm -1)+o(λwm -1-qm -1),
θ22=1+rm -1(λwm -1-qm -1)=rm -1(λwm -1-qm -1)+o(rm -1(λwm -1-qm -1)),
θ23=rm -2+rm -1rm -2(λwm -1-qm -1)=rm -1rm -2(λwm -1-qm -1)+o(rm -1rm -2(λwm -1-qm -1)),
θ31=λwm-qm+rm -1(λwm-qm)(λwm -1-qm -1)=
rm -1(λwm-qm)(λwm -1-qm -1)+o(rm -1(λwm-qm)(λwm -1-qm -1)),
θ32=2(λwm-qm)+rm -1(λwm-qm)(λwm -1-qm -1)=
rm -1(λwm-qm)(λwm -1-qm -1)+o(rm -1(λwm-qm)(λwm -1-qm -1)),
θ33=2rm -2(λwm-qm)+rm -1rm -2(λwm-qm)(λwm -1-qm -1)=
rm -1rm -2(λwm-qm)(λwm -1-qm -1)+o(rm -1rm -2(λwm-qm)(λwm -1-qm -1)).
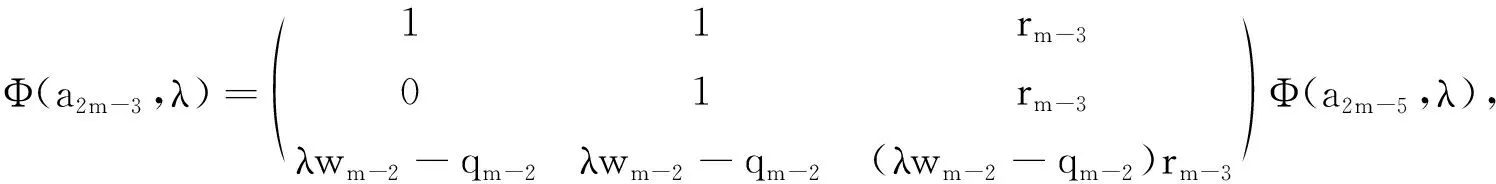
η11=θ11+(λwm -2-qm -2)θ13=rm -1rm -2(λwm -1-qm -1)(λwm -2-qm -2)+
o(rm -1rm -2(λwm -1-qm -1)(λwm -2-qm -2)),
η12=θ11+θ12+(λwm -2-qm -2)θ13=rm -1rm -2(λwm -1-qm -1)(λwm -2-qm -2)+
o(rm -1rm -2(λwm -1-qm -1)(λwm -2-qm -2)),
η13=rm -3θ11+rm -3θ12+rm -3(λwm -2-qm -2)θ13=rm -1rm -2rm -3(λwm -1-qm -1)(λwm -2-qm -2)+
o(rm -1rm -2rm -3(λwm -1-qm -1)(λwm -2-qm -2)),
η21=θ21+(λwm -2-qm -2)θ23=rm -1rm -2(λwm -1-qm -1)(λwm -2-qm -2)+
o(rm -1rm -2(λwm -1-qm -1)(λwm -2-qm -2)),
η22=θ21+θ22+(λwm -2-qm -2)θ23=rm -1rm -2(λwm -1-qm -1)(λwm -2-qm -2)+
o(rm -1rm -2(λwm -1-qm -1))((λwm -2-qm -2)),
η23=rm -3θ21+rm -3θ22+rm -3(λwm -2-qm -2)θ23=
rm -1rm -2rm -3(λwm -1-qm -1)(λwm -2-qm -2)+o(rm -1rm -2rm -3(λwm -1-qm -1)(λwm -2-qm -2)),
η31=θ31+(λwm -2-qm -2)θ33=rm -1rm -2(λwm-qm)(λwm -1-qm -1)(λwm -2-qm -2)+
o(rm -1rm -2(λwm-qm)(λwm -1-qm -1)(λwm -2-qm -2)),
η32=θ31+θ32+(λwm -2-qm -2)θ33=rm -1rm -2(λwm-qm)(λwm -1-qm -1)(λwm -2-qm -2)+
o(rm -1rm -2(λwm-qm)(λwm -1-qm -1)(λwm -2-qm -2)),
η33=rm -3θ31+rm -3θ32+rm -3(λwm -2-qm -2)θ33=rm -1rm -2rm -3(λwm-qm)(λwm -1-qm -1)·
(λwm -2-qm -2)+o(rm -1rm -2rm -3(λwm-qm)(λwm -1-qm -1)(λwm -2-qm -2)).

(18)
再结合引理4中的结果(Φ(b,λ)=Ψ(b,λ)GΦ(c,λ))可得:
(19)

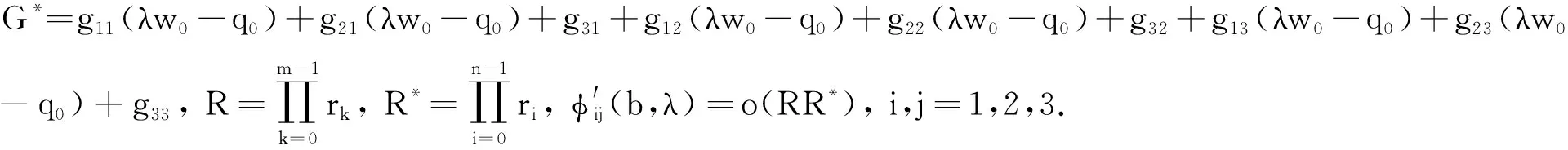
定理1设m,n∈N,g12≠0, 且式(8)—(10)成立,H(λ)=(hij(λ))3 ×3与引理1中的定义一致,则问题(1)至多有m+n+2个特征值.

下面考虑区别于式(1)的另一类情形,即:
由式(1)和式(2)可知,两类含谱参数问题的区别仅是对方程中py″和py′的求导不同,即式(1)中是对py″求一阶导数,而式(2)中是对py′求二阶导数,因此在证明过程中仅给出各自方程等价系统的矩阵形式即可.故令u1=y,u2=y′,u3=py″, 由此可得与方程(py″)′+qy=λwy和(py′)″+qy=λwy等价的系统为:
u′1=ru2,u′2=u3,u′3=(λw-q)u1.
(20)
由于证明式(2)的方法与证明式(1)的方法相似,故本文在此省略.其中的区别是:在系统(20)中,u1在r恒等于零的子区间上是常数,u3在q和w恒等于零的子区间上是常数.
猜你喜欢边值问题三阶特征值三阶非线性微分方程周期解的非退化和存在唯一性数学物理学报(2022年2期)2022-04-26一类内部具有不连续性的不定Strum-Liouville算子的非实特征值问题数学物理学报(2021年6期)2021-12-21一类带强制位势的p-Laplace特征值问题数学物理学报(2021年5期)2021-11-19临界Schrödinger映射非齐次初边值问题的有限差分格式数学物理学报(2021年5期)2021-11-19基于一类特殊特征值集的扩散算子逆谱问题数学物理学报(2021年3期)2021-07-19单圈图关联矩阵的特征值烟台大学学报(自然科学与工程版)(2021年1期)2021-03-19带有积分边界条件的奇异摄动边值问题的渐近解数学物理学报(2020年5期)2020-11-26新型三阶TVD限制器性能分析北京航空航天大学学报(2017年4期)2017-11-23巧填三阶幻方中学生数理化·七年级数学人教版(2017年2期)2017-03-25三阶微分方程理论国外科技新书评介(2014年12期)2015-01-05