尹海鹏,李有堂,黄 华
(兰州理工大学机电工程学院,甘肃 兰州 730050)
颗粒复合材料是典型的非均质、多相、多尺度复合材料,广泛应用于工程领域.集料是颗粒复合材料的重要组成部分和主要承力结构,其几何形态学特性,如形状、棱角性、表面纹理等具有显著的不规则性、无序性和自相似性,并影响集料的空间骨架、级配、空隙及多相间相互作用,进而影响复合材料宏观力学性能[1]、疲劳断裂特性[2-3]等.颗粒复合材料[4]因动态性能稳定、热稳定性好等优点在高速、高档数控机床上得到大量应用,但受集料设计技术的影响,集料几何形态引起的动力及随机损伤演化[5]过程还缺乏研究,限制了该材料的进一步应用.
目前,研究中通常采用刚性球代替集料进行简化分析,忽略了不规则集料的形状和棱角引起的咬合互锁效应.因此,尹纪财[6]在二维层面将盘状颗粒简化为正多边形,验证了集料形状对阻裂作用和强度的影响,但忽略了集料几何形态学特性的不规则性和无序性.超二次曲面法[7]、B样条曲线法[8]虽能够创建无序、不规则的卵石类集料,但难以创建破碎类集料的棱角性和纹理特性,而颗粒捆绑法[9]、球体切割法[10]、立方体切割法[11]、六面体切割法[12]、凸包算法[13]虽然综合考虑了集料形状和棱角性,但仍忽略了集料的纹理特性.针对该问题,Markauskas等[14]用多球体接触间隙代替集料表面纹理,一定程度上能满足对集料纹理特性的研究,但对集料纹理的无序性缺乏研究.张徐等[15]借助激光扫描仪捕获集料表面上的点云数据来重构天然破碎集的纹理特性,但受设备分辨率所限,仍难以构造出的0.1 mm以下的集料表面纹理[16].在此基础上,利用光学显微镜[17]或者基于工业CT扫描和图像处理[18]虽然能够创建足够精细的数字集料,但对设备要求较高,不具有普适性.另一方面,为了控制数字建模成本,秦雪[19]用磨削技术代替工业CT断层扫描,但该方法创建的数字集料精度受磨削厚度影响较大,且随磨削厚度的减小或集料粒径的增大其应用更加局限.
集料的几何形态学特征对颗粒复合材料宏、细观性能的影响显著,亟需开发低成本、高精度的数字集料设计技术.但现有的集料建模技术仍存在以下问题:1)缺乏高效率、高精度、低成本并能兼顾集料的形状、棱角性、纹理特性的集料设计技术;
2)考虑到颗粒复合材料的随机性和无序性,采用逆向重构技术“精确还原”单一集料的几何形态学特征或颗粒复合材料的细观参数,使之应用于其他模型,但缺乏必要性和合理性;
3)获取的几何形态学参数随机性较大,缺乏可重复性,很难定量考察几何形态学特征单一变量对复合材料宏观性能的影响.因此,本文提供一种考虑集料的微、细观特征单一集料建模技术,采用“颗粒替换法”生成宏观颗粒复合材料数字模型,并进一步讨论3D Max中几何形态控制参数对几何形态学评价指标的影响,创建的高精度集料及颗粒复合材料数字模型为深入研究集料几何形态学参数提供基础.
集料在颗粒复合材料内质量分数高达80% ~90%,其理化特性、形态学特性、破碎方法、尺寸效应等很大程度上决定了颗粒复合材料的综合性能,其中尤其以形态学特性最为重要.量化集料的形态学特性是研究形态学参数对颗粒复合材料动力过程和损伤演变的前提,本文从形状、棱角、纹理和集料系统方面对集料进行评价.
1.1 形状评价
形状特征反映集料宏观整体的变化,通常采用圆形度、球形度、细长比、扁平度[20]来量化评价集料的形状.
圆形度R由式(1)定义.

式中:L为集料在空间三个投影视图上的轮廓周长;
S为投影轮廓区域面积.
显然,R越接近1,集料的投影轮廓越接近于圆;
R越接近 1/π2,集料越接近于针状.
球形度D用式(2)定义.

式中:Dmax、Dmin和Dmid分别为集料空间最小包围六面体三边尺寸
的最大值、最小值和中间值.
D越接近1,说明集料越接近于等维,并且随表面面数的增加集料越接近球状.
细长比Er和扁平比Fr分别为

Er越接近0,说明集料越接近于条状;
Fr越接近0,说明集料越接近于片状;
Er、Fr同时越接近1,说明集料越接近等维.
1.2 棱角性评价
棱角性反映集料细观局部的变化,对于轮廓参数相同的粗集料,其表面积、体积很大程度上取决于集料的棱角性,故可以用投影面周长与等效椭圆或最小包络椭圆周长差异评价集料的棱角性,基于周长的棱角性评价指标Ac[20]定义为

式中:Pc为包络凸面周长;
Pe为等效椭圆周长,其值等于式(2)中长轴为Dmax、短轴为Dmin的椭圆周长.
考虑到粗集料棱角性的本质是集料轮廓线上各点半径变化引起的,也可根据给定局部角度变化范围内投影面轮廓半径和等效椭圆半径差异来评价棱角性,基于半径的棱角性评价指标Ar[20]可用式(6)定义:

式中:Rθ为集料投影面轮廓上任意角度 θ时的半径;
Reθ为集料等效椭圆上角度 θ时的半径;
∆θ为相邻两测量之间的角度差.
显然,基于半径的粗集料棱角性精度取决于 ∆θ的取值,∆θ越大,越不能对集料的棱角性做出准确评价,∆θ越小,需要处理的数据越多.式(5)、(6)中参数示意如图1所示[20].

图1 集料等效椭圆和包络图面示意Fig.1 Equivalent ellipse and envelope diagram of aggregate
1.3 表面纹理评价
表面纹理反映集料表面微观结构的变化,集料表面的纹理可视为随机变化的分形波,如图2所示[17].与光滑纹理的骨料相比,带有粗糙纹理的骨料可提高颗粒复合材料宏观力学性能[21],相较于形状和棱角性,集料纹理的评价更复杂,一般有两类:1)视集料表面纹理为随机分形波,基于波形参数评价;
2)基于纹理变化引起的表面积或体积变化评价.

图2 集料表面纹理特性示意Fig.2 Texture characteristics of aggregate surface
对形状和棱角性参数相同的集料,其表面积和体积很大程度上取决于集料表面纹理的粗糙程度,故采用数字集料包络网格的表面积和体积比量化表面纹理,纹理评价指标T为

式中:Vw为数字集料包络网格的体积;
Sw为数字集料包络网格的表面积.
1.4 集料系统评价
仅考虑单个集料的几何形态学特性缺乏现实意义,同一粒径下单个集料几何形态学特征的显著变化一般不会影响颗粒复合材料宏观性能,因此,考虑集料系统的评价更为重要.但传统的几何学难以对多级级配组成的颗粒复合材料骨架系统进行描述,而分形几何[20]被广泛用于研究多尺度、不规则、不连续、自相似的对象,虽然分形理论常被用来研究颗粒复合材料集料级配方案[4],但将集料系统的几何形态学特性作为颗粒复合材料评价指标的研究相对较少.进一步考虑到同一产地、同一加工方式形成的集料在形状、棱角性和纹理特性在统计学上有显著的自相似性,因此,可定义某一筛孔直径下的集料质量分布的分形函数[4]为

式中:x为集料粒径;
mx为集料粒径小于x时的集料质量;
M为集料系统的总质量;
xmax、xmin分别为集料系统中最大、最小集料粒径;
F为分形维数.
骨架型结构的集料系统造成的空隙是由粉末状填料和流体状树脂胶填充,微观尺度上存在最小粒径无限接近0的颗粒,因此,可假设xmin=0,故式(8)可简化为
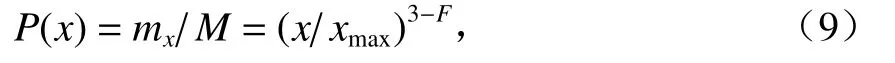
等式两边取对数,整理得:

式中:α=(F−3)lgxmax.
由式(10)可知:对数坐标下 lg (mx/M) 与 lgx存在线性关系,即给定分形维数,必然有确定的集料系统与之对应;
反之,给定集料系统必然有满足该集料系统的分形维数,因此,采用分形维数评价骨料系统有稳定性和可行性.
不规则集料间的动力过程、低流动性和咬合互锁效应显著影响颗粒复合材料的宏观力学性能[8],集料几何形态的量化评价为集料的合理分类和质量控制提供了依据,但对不规则集料几何形态特征的精细设计仍是细观力学研究的重要问题.目前,常用的集料建模技术效率较低或精度不足,而基于3D Max设计不规则集料几何形态具有显著优势,如图3所示.

图3 3D Max中集料几何特征的实现Fig.3 Realization of geometric characteristics of aggregate in 3D Max
3D Max中细观层面上的形状和棱角性可以通过基体尺寸、基体分段数(number of subsections of element edges,Ns)、球形化指数(spherify,Sp)、置换强度(displace,Di)、自由变换(free form deformation,Ff)等修改参数实现;
微观层面上的纹理特性可通过涡轮平滑迭代次数(turbine smoothing,Ts)、噪波强度(noise,Ni)、噪波粗糙度(roughness,Ro)等参数修改.因此,灵活应用上述微、细观特征修改参数,可设计任意不规则集料几何形态特征.
针对破碎类集料明显的不规则形状、棱角性和表面纹理,用图4(a)的步骤设计,而卵石类集料可忽略棱角性和表面纹理,用图4(b)的步骤设计.专业优化(Op)修改器可在保证集料表面积和体积不变的情况下,以牺牲纹理特征为代价对集料的包络网格控制点进行优化,如图5所示.
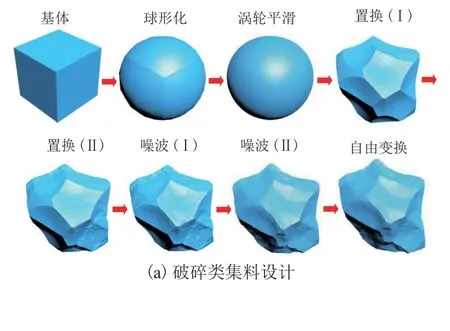
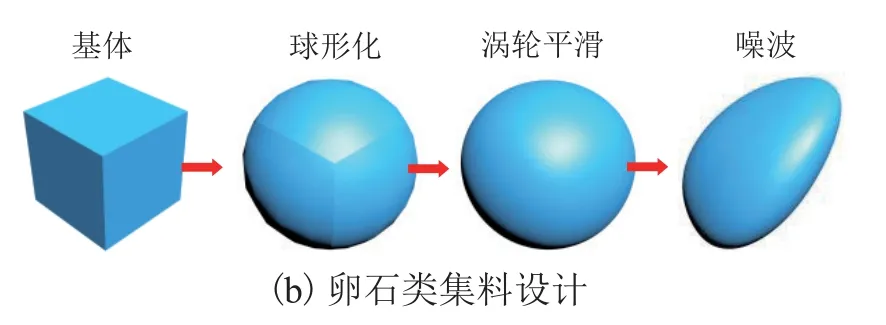
图4 不规则集料在3D Max中的创建步骤Fig.4 Steps of creating irregular aggregate in 3D Max

图5 3D Max优化工具对集料控制网格的影响Fig.5 Influence of 3D Max optimization tool on aggregate wrap mesh
单一集料数字模型在离散元软件中装配后获得颗粒复合材料数字模型,装配空隙率直接影响装配颗粒的数量、颗粒配位数、仿真时间和数值分析结果等.但同一集系统的实物模型和数字模型空隙率差异较大,这主要是因为数字模型通常只考虑集料骨架系统建模,而实物模型集料骨架系统造成的空隙由填料和黏结剂填充.另外,最小颗粒粒径差异也可能引起两种模型空隙率的不同.因此,研究两种模型空隙率转化关系创建精细颗粒复合材料数字模型更重要.
3.1 数字模型的空隙率
集料形状和棱角性是集料骨架形成空隙的决定因素,对颗粒复合材料的宏观性能有重要的影响.已有研究表明:颗粒复合材料集料系统形成的空隙、集料的表面积、集料系统的体积也具有分形特性[22-23],并且集料系统的分形维数与空隙率的分形维数之间存在必然的内在联系[24].根据分形定义,集料系统引起的体积分形可表达为[23]

式中:Vx为粒径小于x时集料的分形体积;
V为集料系统的分形总体积;
Fv为体积分形维数.
集料粒径在(x,x+dx)区间上的分形体积为

由实体体积定义:

式中:ρ为集料表观密度.
联立式(8)、(12)、(13),并在集料粒径区间(xmin,xmax)上积分,得任意粒径x时的分形体积Vx为
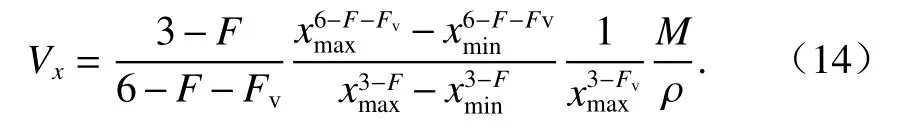
由空隙率p的定义知:

式中:Vtot为建模体积.
集料系统形成的空隙率只与最大粒径xmax、最小粒径xmin、集料的质量M、表观密度 ρ、建模体积Vtot以及集料级配分形维数F、体积分形维数Fv有关.考虑到离散元模型中,集料最小粒径xmin是一个不能忽略的确定值,故式(15)为创建离散元模型时的空隙率提供了可靠的理论支撑.同理,令xmin=0,式(15)可简化为

式中:pd为颗粒复合材料空隙率的理论值.
颗粒复合材料空隙率的实际值pt为

式中:Vair为实物模型空隙体积;
ρe为颗粒复合材料的等效密度;
ρr为各项相材料总质量与颗粒复合材料体积的总比值.
令pd=pt,联立式(10)、(16)、(17)得到集料的体积分形维数Fv.进一步将集料系统的分形维数F、体积分形维数Fv、建模时最大粒径xmax和最小粒径xmin代入式(15),可获得颗粒复合材料创建离散元模型时的空隙率p.
3.2 颗粒复合材料数字模型创建技术
空隙率p为采用颗粒流程序(particle flow code,PFC)命令流ball distribute生成颗粒复合材料离散元模型提供可靠的理论依据,但相较于球形颗粒,不规则集料的形态特征引起的细观动力过程更复杂,在采用第三方建模软件生成的不规则集料时很难满足平衡条件.因此,采用“颗粒替换法”生成颗粒复合材料数字模型,颗粒间设置平行黏结接触并计算平衡,具体步骤如下:
1)按级配方案生成球状颗粒,计算至平衡;
2)按粒径范围遍历要替换的球状颗粒的质心位置、体积、密度、半径;
3)在球状颗粒的同一位置生成等体积、等密度的不规则颗粒,并删除球状颗粒;
4)利用随机函数使不规则颗粒在同一位置转动任意角;
5)根据接触条件搜索悬浮颗粒,利用逐步膨胀法分步放大悬浮颗粒粒径直到满足配位数要求并重新计算至平衡.
该方法可在同一颗粒复合材料数字模型中生成多种不规则颗粒,有效降低不规则颗粒的接触动能,并快速达到初算平衡.基于分形理论,F=2.6,粒径分布为(0, 0.30]、(0.30, 0.60]、(0.60, 1.18]、(1.18, 2.36]、(2.36, 5.00]mm,实际空隙率为16.0%,修正空隙率为35.8%,用同一种不规则颗粒替换x≥ 1.18 mm时的颗粒,复合材料三维离散元模型如图6所示.
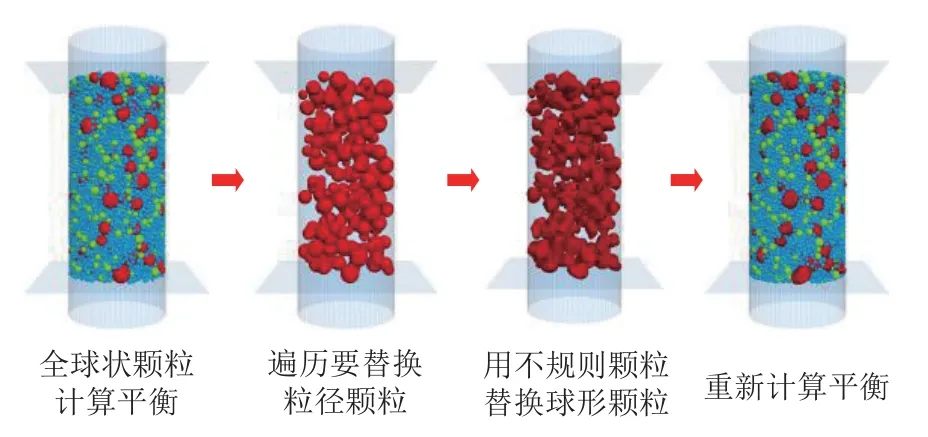
图6 颗粒复合材料数字模型Fig.6 Discrete element model of particle composite
4.1 建模参数变量对集料精度的影响
基体分段数、涡轮平滑迭代次数和PFC 3D刚形颗粒簇建模参数是影响集料精度和数值分析时间成本的主要因素,集料精度试验方案参数设置如表1所示.在颗粒重叠量(distance)为130、填充颗粒最大与最小粒径比(ratio)为0.5时,考察颗粒簇包络网格导入PFC创建刚性颗粒簇的时间成本.如图7所示,随着基体分段数和涡轮平滑迭代次数的增加,集料包络网格控制点数量增大,并且涡轮平滑迭代次数引起的网格控制点增加速度更明显.
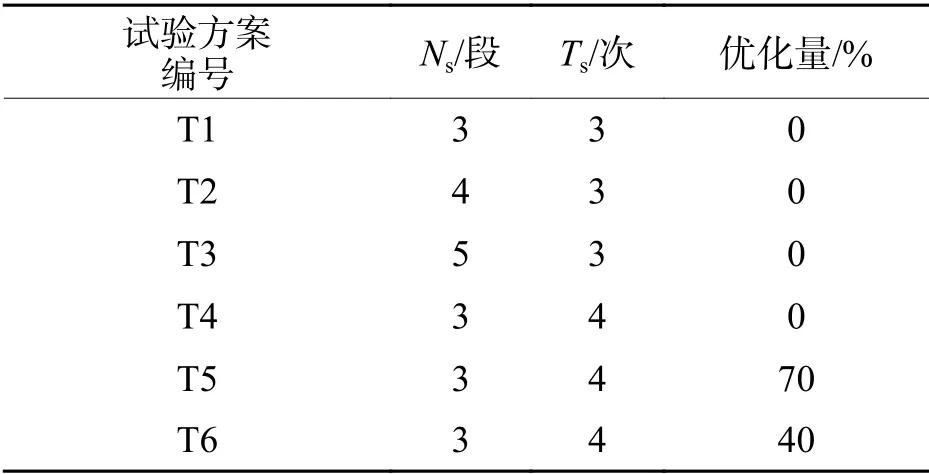
表1 集料建模精度试验方案Tab.1 Accuracy test schemes of aggregate modeling

图7 基体分段数和涡轮平滑迭代次数对颗粒簇包络网格节点的影响Fig.7 Influence of numbers of segments and turbo smooth iterations on wrap mesh nodes
网格控制点影响颗粒簇包络网格导入PFC的效率,如图8所示,网格控制点数量与导入时间成本正相关,填充颗粒簇包络网格的球状颗粒数量与集料纹理特性没有关系.进一步研究表明,创建PFC 3D颗粒复合材料数字模型时,Ns=3段,Ts=3次是创建颗粒簇包络网格的一个理想参数,优化网格控制点可在不影响颗粒填充效果的情况下显著提高数值分析效率.

图8 不同试验方案下的集料精度和数值分析效率Fig.8 Aggregate accuracy and numerical analysis efficiency under different test schemes
4.2 建模参数对集料表面积和体积的影响
以Ns=3段,Sp=100%,Ts=3次,Di=2.0mm,Ni=0.1mm为对照参数创建数字集料模型,讨论单一建模变量对数字集料模型体积和表面积的影响.如图9所示,集料的建模参数中,基体分段数、球形化指数、置换强度对集料表面积和体积的影响相较于涡轮平滑迭代次数、噪波强度、噪波粗糙度更加敏感,并且涡轮平滑迭代次数、噪波强度、噪波粗糙度对集料表面积的影响相对于其对集料体积的影响更加敏感.研究表明,基体分段数、置换强度、球形化指数对集料空间尺寸影响较大,主要用于构造如集料的轮廓、形状、棱角性这些细观几何形态学特征,但涡轮平滑、噪波强度、噪波粗糙度对表面纹理影响较为显著,主要用于构造集料的微观几何形态学特征.另外,随着基体分段数和置换强度的增加,集料的表面积和体积均增加,但球形化指数增加导致集料的表面积和体积减小,这是因为基体分段数和置换强度主要通过拉伸网格控制节点来增大基体空间,进而构建棱角分明的集料,而球形化修改则主要用于弱化集料的棱角,并使集料尽可能扭曲为球状颗粒.

图9 建模参数对集料表面积和体积的影响Fig.9 Influence of modeling parameters on aggregate surface area and volume
4.3 纹理评价指标稳定性分析
如图10所示,随着噪波强度、噪波粗糙度、涡轮平滑迭代次数的增大,纹理评价指标均减小,但噪波粗糙度对纹理评价指标的影响最为显著,这是因为噪波粗糙度的增加使集料网格控制节点的凸起或凹陷越明显,即纹理分形波的振幅更加显著.曲线的单调性表明,给出的式(7)评价集料纹理具有可行性和稳定性.
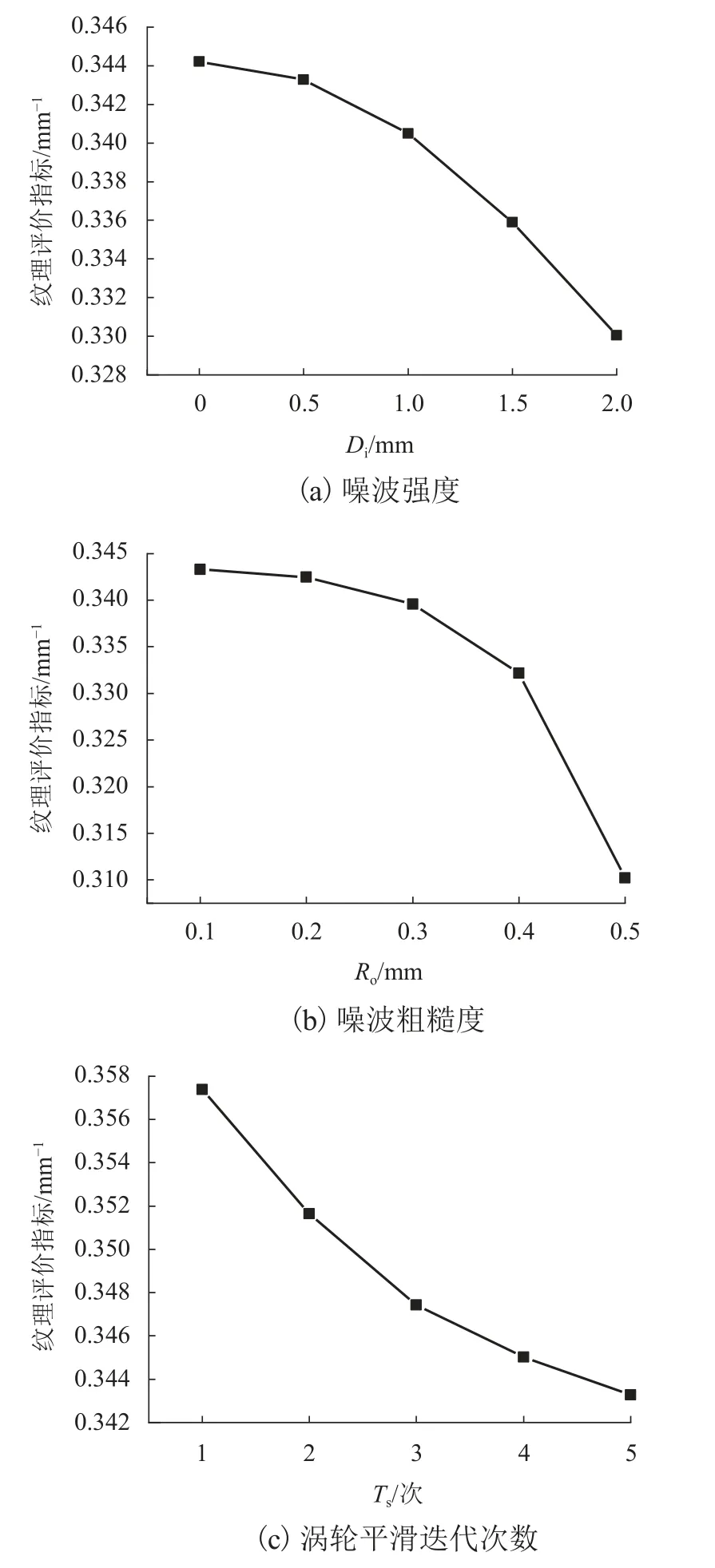
图10 纹理构造参数对纹理评价指标的影响Fig.10 Influence of texture construction parameters on texture index
4.4 集料几何形态特征对颗粒复合材料力学性能的影响
尹纪财[6]以“济南青”花岗岩为试验集料,用5级级配实验了不同最大粒径下的树脂基颗粒复合材料(resin matrix composite, RMC)的单轴抗压强度,本文以最大粒径为5.00 mm时的最大抗压强度116 MPa为参照,用平行黏结接触模型考虑树脂与集料的黏结作用,用“颗粒替换法”在参照样本的同一位置用任意几何学特性的不规则集料分别替换最大一级粒径和最大两级粒径的圆形集料,考察集料综合几何学特性对RMC抗压强度的影响.如图11所示,用不规则颗粒替换x≥ 2.36 mm的球形颗粒,可使RMC的峰值抗压强度提高20.7%,且替换的球形颗粒越多,RMC的峰值抗压强度提高越显著,但颗粒复合材料内部集料的几何学特性越复杂,压缩破坏时峰值抗压强度越不稳定,可能会出现多个局部峰值强度.研究表明,集料的几何学特征能显著提高集料之间的咬合互锁效应,进而表现为单轴压缩试验中RMC抗压强度的提高.

图11 集料几何学特性对RMC抗压强度的影响Fig.11 Influence of aggregate geometric properties on RMC compressive strength
针对现有数字集料设计技术不足,基于3D Max和PFC联合创建单一集料和颗粒复合材料的数字模型,量化并拓展了几何形态特性评价指标,进一步研究了实物模型和数字模型空隙率转化关系,主要结论有:
1)与现有方法相比,基于3D Max的数字集料设计技术能兼顾集料的形状、棱角性和纹理特性,并具有参数可控、精度和效率高、适应性广等显著优势.基体分段数、球形化指数和置换强度主要用于构造集料的宏-细观几何形态学特征,而涡轮平滑迭代次数和噪波参数则主要用于构造集料表面的微观纹理特征.
2)提供了一种评价集料表面纹理的方法,丰富了集料纹理评价的数学模型.该数学模型能稳定地表征集料表面纹理;
同时考虑宏、细观辩证关系,利用分形维数评价颗粒复合材料骨料系统的方法,拓展了集料几何形态学评价指标.
3)考虑颗粒复合材料数字模型与实物模型中最小粒径的差异,基于分形几何理论研究了颗粒复合材料数字模型的空隙率.同一粒径分布区间下数字模型和实物模型空隙率存在较大差异,进而给出空隙率转化的数学模型,为颗粒复合材料的精细建模提供可靠的理论依据.
4)采用“颗粒替换法”能全部或部分替换不同粒径区间的球形颗粒,创建带有几何形态特征的颗粒复合材料数字模型,为集料几何形态参数定向、定量研究提供了基础,并有效提高数值分析效率.
猜你喜欢数字模型棱角空隙数字模型分析在垂直型食物嵌塞治疗中的应用口腔医学(2021年10期)2021-12-02美国太空部队与工业部门分享内部数字模型军民两用技术与产品(2021年9期)2021-03-09曝光智族GQ(2019年11期)2019-11-15处世之道意林(2019年20期)2019-10-24空隙满族文学(2019年5期)2019-10-08排水性沥青路面的横向空隙分布特性江苏大学学报(自然科学版)(2018年6期)2018-11-15观山智族GQ(2018年10期)2018-05-14善待有棱角的干部当代陕西(2017年12期)2017-08-15北京楼市新政封堵防炒作空隙领导决策信息(2017年14期)2017-06-213D打印数字模型的独创性认定现代商贸工业(2016年24期)2017-01-13